大家好，我~~会打表找规律切题我很自豪~~。

前言

在 OI 中，很多一类计数题或其它题有这样的特征：

输入数字只有一个或两个。

~~考场上如果看到这种题，想个鬼正解，直接使用高级算法：打表找规律！！！！！~~

（近期模拟赛大致有三四道题，有的是打表找出递推式拿部分分，有的是直接找出正解，所以来水写这篇文章啦）

前置技能

碰到这样的题，八成会给你这样数据范围：

对于 $10\%$ 的数据，$n,m\le 10$ $\cdots$

那么，第一步，首先打一个最暴力的暴力！

然后，我们直接把表打出来，就比如这样：

for (int n = 1; i <= 10; i++) {
    for (int m = 1; m <= n; m++) {
        printf("%d ", solve(n, m));
    }
    printf("\n");
}

这样我们就能得到一个这样的表了（以组合数举例）：

1
1
2 1
3 3 1
4 6 4 1
5 10 10 5 1
6 15 20 15 6 1
...

~~它对不齐，丑死了！！！~~

我们改变一下输出方式：

for (int n = 1; i <= 10; i++) {
    for (int m = 1; m <= n; m++) {
        printf("% 5d ", solve(n, m));
    }
    printf("\n");
}

  1
 1
 2   1
 3   3   1
 4   6   4   1
 5  10  10   5   1
 6  15  20  15   6   1
...

这样规律就比较好找了。

~~啊我觉得它还是丑！！！~~

这时候，我们就要请我们的 ~~Excel 上场了！~~

显然不太行，我反正不会用 C++ 读写 Excel 表格。

但是我们有这样一个神奇的文件类型：.csv。

逗号分隔值（Comma-Separated Values，CSV，有时也称为字符分隔值，因为分隔字符也可以不是逗号），其文件以纯文本形式存储表格数据（数字和文本）。纯文本意味着该文件是一个字符序列，不含必须像二进制数字那样被解读的数据。

具体怎么用呢？

我们把上面那个程序改改：

for (int n = 1; i <= 10; i++) {
    for (int m = 1; m <= n; m++) {
        printf("%d,", solve(n, m));
    }
    printf("\n");
}

1,
1,1,
1,2,1,
1,3,3,1,
1,4,6,4,1,
1,5,10,10,5,1,
1,6,15,20,15,6,1,
...

我们把它保存在 table.csv 里面，再用 Excel 或者任何你有的可以打开表格的软件打开：

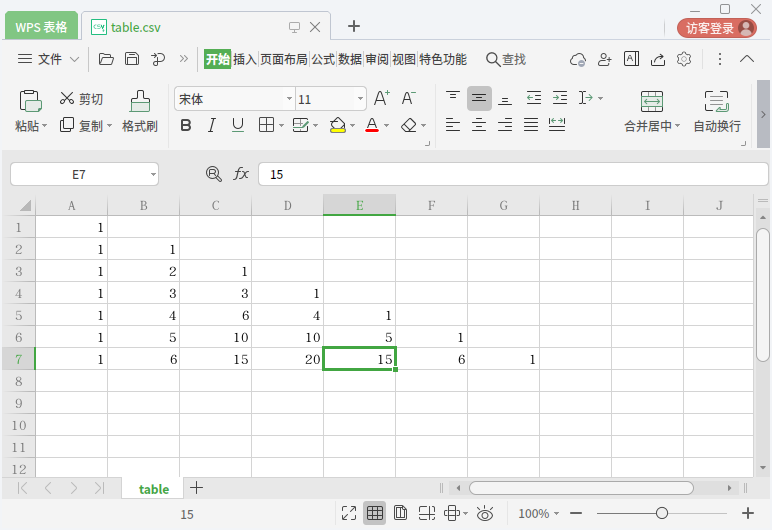
你会发现它就变成表格了！

然后你就可以方便的使用 Excel 公式进行一些操作了，比如求差等。

寻找递推关系

很多这种题都会存在一种递推关系。普通的递推关系可能不太好看，但是如果我们放到表格上，就好看多了。比如最基本的杨辉三角，就是每一个数等于它上面的数与它左上角的数的和。

我们来看一个简单的例子：

          
1          
1  1        
1  3   1      
1  7   6   1    
1  15  25  10  1  
1  31  90  65  15  1

请一眼看出来的先闭嘴。

我们来考虑类似于杨辉三角的方式，观察每个数与它上面的数和它左上角的数的关系：

首先发现，第三列不就是 $2^n-1$ 的形式嘛？我们换一种思路考虑：其实这一列就是上面的数乘 $2$ 再加上左上角的数。我们再来看第四列：发现这种规律不适用了。但是！比如我们拿 $25$ 来说，$6\times 2 + 7 = 19$，我们发现这个数刚好差出了上面的那个数。于是，我们可以得出，第四列的每个数等于它上面的那个数乘 $3$ 加上左上角的数。

于是我们就可以猜测了：第 $k$ 列的数就是它上面的数乘 $k - 1$ 加上左上角我的数。

实际上这就是第二类斯特林数的递推公式。

那么我们考场上如何验证这个东西呢？

我比较喜欢直接拿 Excel 的公式自动填充来写，不过直接写个代码验证好像也不麻烦。

不过，我们发现，许多这样的式子都和它所在的行号、列号有关，所以我们最好在打表的时候把行号、列号也输出出来。

我们来看个比较难的例题：（其实是前几天考试的一道题）

    2       3       4       5       6       7       8
 1
 1      1 
 1      3       2 
 1      7      11       5 
 1     15      43      45      16 
 1     31     148     268     211      61 
 1     63     480    1344    1767    1113     272 
 1    127    1509    6171   12099   12477    6551    1385 

什么东西啊？？

首先发现第二列还是 $2^n-1$ 的形式，也许和上一次类似，比如这个数是上面的数的多少倍加左上角的数之类的。

然后看第三列：好怪哦，这什么东西？？

我们尝试套用上一列的公式：$2\times 3 + 3 = 9,11\times 3 + 7 = 40,43\times 3 + 15=144$。发现是上一行的数乘 $3$ 加上左上角的数加上了一个数，准确来说是 $f_{i,3}=f_{i-1,2}+3\times f_{i-1,3} + i - 2$。

那么第四列呢？$5\times 4 + 11=31,45\times 4 + 43=223,268\times 4 + 148=1220$ 这差太多了吧！

不要慌，我们看看差多少：$45-31=14=2\times 7,268-223=45=3\times 15,1344-1220=124=4\times 31$。这不就是第二列的数吗？

于是我们猜测一个这样的式子：

\[f_{i,j}=f_{i-1,j-1} + j\times f_{i-1,j} + (i - j + 1) * f_{i-1,j-2}\]

验证几个。芜湖，是对的！

然后你就得到了 $O(n^2)$ 的式子。

跑路啦

高阶技能 1：高阶差分

众所周知，一个多项式函数若干次差分之后，就会变成一个常数。

所以，我们可以先给它差分上~~几百次~~，看他是不是常数。

然后直接暴力拉格朗日插值 XD

练习题：P4463

高阶技能 2：卡特兰数

众所周知，卡特兰数是 $1,1,2,5,14,42,132$

我们看到这个东西就可以开始往卡特兰数的方向想了。

又众所周知，卡特兰数可以写成 $\binom{2n}{n} - \binom{2n}{n-1}$，这东西就可以拓展到二维了。

所以，有时候在二维表中遇到卡特兰数时，就可以直接用这个式子来套。