想到了一种不使用普通的求最大权闭合子图的方法,貌似也可以推广到求最大权闭合子图上,不过就是建模更复杂计算更麻烦然后也没有什么优势罢了。
本题的目标为,制定一套 Zombies 的进攻方案,选择进攻哪些植物以及进攻的顺序,从而获得最大的能源收入。
考虑构建最小割模型,将所有正数和负数分开考虑,如果一个正数不选就会造成损失,如果选一个负数就会造成其绝对值的损失,这样求最小损失,再用所有正数之和减去最小损失就是最大收入了。
接下来就是我的奇怪建模了
因为发现,如果要击溃一个位置的 Plant,那么在它右面的所有 Plant 都要被击溃,所以我们可以考虑每一行上被击溃了的 Plant 的区间左端点。那么这一行的损失,就是这个左端点向右(包括左端点)的所有负数的绝对值之和加上左端点向左(不包括左端点)的所有正数之和。
发现这个权值很容易就可以利用前缀和和后缀和处理出来,于是我们就可以构建这样一个模型:
设 $r_{i,j}$ 为从 $(i,j)$ 开始向右的所有负数的绝对值之和,$l_{i,j}$ 为从 $(i,j)$ 开始向左的正数之和,则可以连边:
\[(i,j)\xrightarrow{\normalsize r_{i,j}+l_{i,j-1}}(i,j-1)\] \[S\xrightarrow{\normalsize l_{i,m}}(i,m)\] \[(i,1)\xrightarrow{\normalsize r_{i,1}}T\]然后考虑如何解决 Plant 攻击的问题。
Plant 攻击的本质是什么?实际上就是如果 $(i,j)$ 保护 $(x,y)$,那么如果 $(i,j)$ 这个植物不被击溃,$(x,y)$ 及向左的所有植物就也都不能被击溃。
放到我们的最小割模型上呢?我们将 $(x,y)$ 向 $(i,j)$ 连一条边,其实就是:如果 $(x,y)$ 向右的边 $A$ 被割,那么 $(i,j)$ 向左的边 $D$ 就没必要割;反之,如果 $(x,y)$ 向左边的边 $B$ 被割,那么 $(i,j)$ 向左的边 $D$ 就也必须割掉。
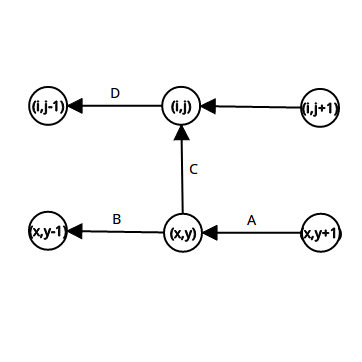
(若还不明白,可以转向 [HNOI2013]切糕,这道题题的距离限制与本题的 Plant 攻击比较相似。)
这样,就实现了 Plant 攻击的限制。
可是这样连样例都过不了。为什么?
样例中,$(3,1)$ 能攻击到 $(3,2)$,这导致第三行的 Plant 不可能被攻击到,但是如果用上图的限制方式,那么他只需要将 $(3,1)\rightarrow T$ 的边割掉就好了,而这显然是不合法的。你不能先跳过去把植物鲨了然后再跳回来嘛
然后我就傻乎乎的去特判了下这种情况,然后拿到了 90 分的好成绩
这种情况的本质是什么?实际上是出现了一个环。除了样例中这种情况,还可能有这样的情况:
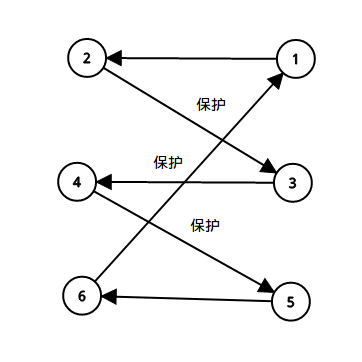
(这里箭头是指 Plant 能攻击到的位置)
那么这显然就是一个环了。如果出现了一个环,我们就将环中所有的点都向 $T$ 连一条 $\infty$ 的边,就可以保证它不被割掉了。
判环我使用的是 Tarjan,于是这题就做完了。
代码:
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1209, MAXM = 1000005;
const int inf = INT_MAX / 2;
struct Graph { // 网络流板子
int fst[MAXN], to[MAXM], f[MAXM], now[MAXN], d[MAXN], nxt[MAXM], tot;
Graph() : tot(1) {}
void add(int u, int v, int w) {
to[++tot] = v, nxt[tot] = fst[u], f[tot] = w, fst[u] = tot;
to[++tot] = u, nxt[tot] = fst[v], f[tot] = 0, fst[v] = tot;
}
int s, t;
bool bfs() {
memset(d, 0, sizeof d);
queue<int> q; q.push(s); d[s] = 1, now[s] = fst[s];
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = fst[u], v = to[i]; i; i = nxt[i], v = to[i]) {
if (f[i] && !d[v]) {
q.push(v);
d[v] = d[u] + 1;
now[v] = fst[v];
if (v == t) return true;
}
}
}
return false;
}
int dinic(int u, int flow) {
if (u == t) return flow;
int rest = flow;
for (int &i = now[u], v = to[i]; i; i = nxt[i], v = to[i]) {
if (f[i] && d[v] == d[u] + 1) {
int k = dinic(v, min(f[i], rest));
if (!k) d[v] = 0;
f[i] -= k;
f[i ^ 1] += k;
rest -= k;
}
if (!rest) break;
}
return flow - rest;
}
int solve() {
int flow, maxflow = 0;
while (bfs())
while (flow = dinic(s, inf)) maxflow += flow;
return maxflow;
}
}g;
int n, m;
int s[55][55], a[55][55][55];
int l[55][55], r[55][55], sum;
int ids(int x, int y) { // 点 ID
return (x - 1) * m + y;
}
int ide(int x, int y) { // 点的左边一个点的 ID
if (y == 1) return g.t;
return ids(x, y - 1);
}
struct Graph2 {
int fst[MAXN], nxt[MAXM], to[MAXM], tot;
int degree[MAXN];
void add(int u, int v) {
to[++tot] = v;
nxt[tot] = fst[u];
fst[u] = tot;
degree[v]++;
}
int dfn[MAXN], low[MAXN], dcnt;
bool inStack[MAXN], vis[MAXN];
stack<int> st;
void tarjan(int u) {
vis[u] = 1;
dfn[u] = low[u] = ++dcnt;
inStack[u] = 1;
st.push(u);
for (int i = fst[u], v = to[i]; i; i = nxt[i], v = to[i]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (inStack[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
int cnt = 0;
vector<int> pts;
while (1) {
int t = st.top(); st.pop();
inStack[t] = 0;
cnt++;
pts.push_back(t);
if (t == u) break;
}
if (cnt > 1) {
for (int t : pts)
g.add(t, g.t, inf);
}
}
}
}g2;
int main() {
scanf("%d%d", &n, &m);
g.s = 2 * n * m + 1, g.t = 2 * n * m + 2;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
int w;
scanf("%d%d", &s[i][j], &w);
if (s[i][j] > 0) sum += s[i][j], l[i][j] = s[i][j];
else r[i][j] = -s[i][j];
while (w--) {
int x, y; scanf("%d%d", &x, &y); x++, y++;
g2.add(ids(i, j), ids(x, y));
a[i][j][x] = max(a[i][j][x], y);
}
}
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
l[i][j] += l[i][j - 1];
for (int i = 1; i <= n; i++)
for (int j = m; j >= 1; j--)
r[i][j] += r[i][j + 1];
for (int i = 1; i <= n; i++)
g.add(g.s, ids(i, m), l[i][m]);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
g.add(ids(i, j), ide(i, j), r[i][j] + l[i][j - 1]);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
for (int k = 1; k <= n; k++) {
int p = a[i][j][k];
if (p) {
g.add(ids(k, p), ids(i, j), inf);
}
}
for (int i = 1; i <= n; i++)
for (int j = 1; j < m; j++) g2.add(ids(i, j + 1), ids(i, j));
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (!g2.vis[ids(i, j)]) g2.tarjan(ids(i, j));
printf("%d\n", sum - g.solve());
return 0;
}
