后缀数组, 即 $sa$ 数组, 代表的是一个字符串所有后缀按照字典序排序后, 排名第 $i$ 的后缀的开头位置。
举个例子:
aabaaab 的所有后缀有:
| 编号 | 前缀 |
|---|---|
| 1 | aabaaab |
| 2 | abaaab |
| 3 | baaab |
| 4 | aaab |
| 5 | aab |
| 6 | ab |
| 7 | b |
我们对他进行排序:
| 排名 | 编号 | 前缀 |
|---|---|---|
| 1 | 4 | aaab |
| 2 | 5 | aab |
| 3 | 1 | aabaaab |
| 4 | 6 | ab |
| 5 | 2 | abaaab |
| 6 | 7 | b |
| 7 | 3 | baaab |
那么此时的编号就是所谓的后缀数组了。
我们记后缀 $i$ 为编号为 $i$ 的后缀, 即从第 $i$ 个字符开始的后缀, 那么 $sa_i$ 就是指排名为 $i$ 的后缀为后缀 $sa_i$。
同时,记 $rank_i$ 为后缀 $i$ 的排名,不难发现 $sa$ 和 $rank$ 是互逆的。
什么意思呢? 形式化来说, $rank[sa_i] = sa[rank_i] = i$。
定义就先讲到这里,接下来我们来考虑如何求这个后缀数组。
求法
$O(n^2)$ 算法
这个算法是很显然的,就按照定义进行排序即可。
$O(n\log^2 n)$ 算法
上述做法的瓶颈在于比较两个字符串的复杂度过高, 我们来考虑优化他。
我们可以考虑这样的一种排序方式:
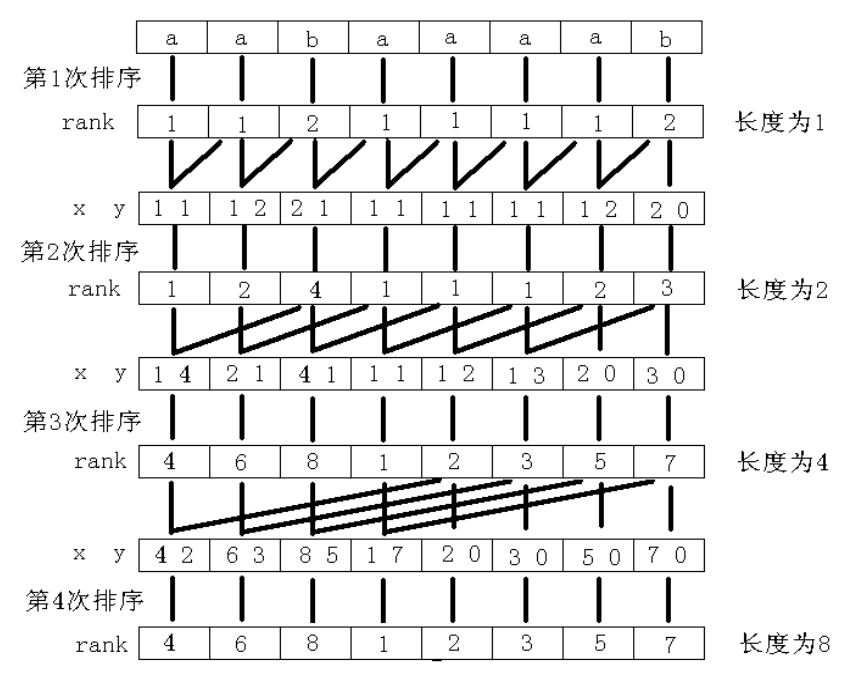
首先将所有长度为 $1$ 的子串进行排序, 再对所有长度为 $2$ 的子串进行排序, 一直这样排序下去。
也就是利用倍增的思想对这个子串进行排序。
因为是字典序最小, 对于一个长度为 $w$ 的子串, 我们可以看做为以前 $\frac{w}{2}$ 个字符作为第一关键字, 以后 $\frac{w}{2}$ 个字符为第二关键字进行排序, 这样一共进行 $O(\log n)$ 次排序, 如果采用朴素的快速排序, 那么总复杂度就是 $O(n \log^2 n)$ 的。
$O(n\log n)$ 算法
这个算法实际上是上一种算法的更进一步的优化。
在讲这个题之前, 我们首先先讲一种排序方式:
基数排序
他的思想大致就是:将要排序的数列的每一个数分为若干部分,对每一部分进行稳定排序。
没关系我也听不懂
看下面的例子:
| 1 | 7 | 3 |
|---|---|---|
| 5 | 2 | 6 |
| 1 | 7 | 8 |
| 5 | 2 | 3 |
首先对第三列进行排序:
| 1 | 7 | 3 |
|---|---|---|
| 5 | 2 | 3 |
| 5 | 2 | 6 |
| 1 | 7 | 8 |
然后对第二列进行稳定排序:
| 1 | 7 | 3 |
|---|---|---|
| 1 | 7 | 8 |
| 5 | 2 | 3 |
| 5 | 2 | 6 |
等等,什么是稳定排序?
看这个排序结果, 你会发现, 对于相同的元素, 原来排在前面的元素排序之后仍然排在前面, 这样就能够保证对于第二列相等的, 第三列仍然是有序的, 因为相同元素的先后顺序没有进行改变, 这样就保证排序是正确的。
那么, 对于每一个关键字应该如何进行稳定排序?
一种稳定排序是归并排序, 但是我们的前提是已经将一个数字分为了好几个数字, 这样就能保证他们的值域足够小, 在复杂度能接受的范围内。
值域小要如何排序?
当然是桶排序(计数排序)!
桶排序也是一种稳定的排序算法,于是我们就完成了基数排序。
先来看一下代码实现:
int a[MAXN], cnt[MAXN], b[MAXN];
int n, m; // m 为值域
void Qsort() {
for (int i = 1; i <= m; i++) cnt[i] = 0;
for (int i = 1; i <= n; i++) cnt[a[i]]++;
for (int i = 1; i <= m; i++) cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--) b[cnt[a[i]]--] = a[i];
}
这什么玩意
第一行循环是清空计数数组,就是桶。
第二行是进行计数。
第三行对计数数组进行了一个前缀和。
这句话什么意思呢?
我们考虑将做完前缀和的数组放到数轴上:
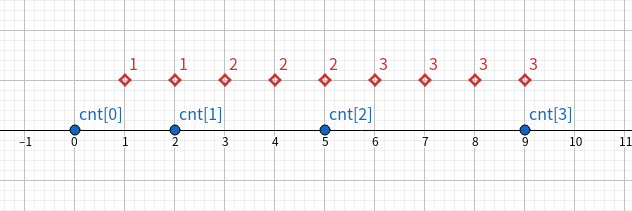 可以发现, 此时 $cnt$ 数组就是代表的每一个连续且相同的数段的最后一个的位置。
此时我们从后往前扫, 每扫到一个就以此时 $cnt$ 的位置作为它排序后的位置, 并把指针向左移动一位, 这样就做到了排序。
可以发现, 此时 $cnt$ 数组就是代表的每一个连续且相同的数段的最后一个的位置。
此时我们从后往前扫, 每扫到一个就以此时 $cnt$ 的位置作为它排序后的位置, 并把指针向左移动一位, 这样就做到了排序。
为什么从后往前扫呢? 此例子中其实从前往后, 从后往前都无所谓, 因为相同元素是完全相同的。 但是我们需要实现的是稳定排序, 也就是相同位置的相对位置不改变。 我们是从前往后将元素加入桶的, 为了保证原顺序不变, 那么应该从右面往左面扫。
那么基数排序如何应用到后缀数组中呢?
我们进行第二关键字排序时, 要排序的数字是它的排名, 也就是值域是 $O(n)$ 级别的。
按照基数排序的思想,我们对每个长度为 $w$ 的序列进行一次基数排序, 也就是先按照后 $\frac{w}{2}$ 个数的排名进行桶排序, 再对前 $\frac{w}{2}$ 个数的排名进行桶排序, 这样就对每个长度为 $w$ 的子串排序完毕了。
首次排序时, 我们可以将每个字符的 ASCII 码作为初始的排名,对排名进行排序。 但是这样有一个问题, 就是排序后得到的排名就会不连续。 并且, 如果排序时有两个相等的子串, 他们的排名应该是相等的。 所以在每轮排序后, 我们要对排名进行去重, 重新标号。
说了这么多, 先来看一组例子:
还用最开头的例子来说:
| 编号 | 前缀 |
|---|---|
| 1 | aabaaab |
| 2 | abaaab |
| 3 | baaab |
| 4 | aaab |
| 5 | aab |
| 6 | ab |
| 7 | b |
- 对第一个字符进行排序:
| 编号 | 前缀 | 排名 |
|---|---|---|
| 1 | aabaaab | 97 |
| 2 | abaaab | 97 |
| 4 | aaab | 97 |
| 5 | aab | 97 |
| 6 | ab | 97 |
| 3 | baaab | 98 |
| 7 | b | 98 |
- 接下来处理长度为 $2$ 的。 我们首先找出所有第一关键字和第二关键字:
| 编号 | 前缀 | 排名 | 第二关键字排名 |
|---|---|---|---|
| 1 | aabaaab | 97 | 97 |
| 2 | abaaab | 97 | 98 |
| 4 | aaab | 97 | 97 |
| 5 | aab | 97 | 97 |
| 6 | ab | 97 | 98 |
| 3 | baaab | 98 | 97 |
| 7 | b | 98 | 0 |
(红色为第一关键字, 绿色为第二关键字, 不够的直接补0)
- 按照第二关键字排序:
| 编号 | 前缀 | 排名 | 第二关键字排名 |
|---|---|---|---|
| 7 | b | 98 | 0 |
| 1 | aabaaab | 97 | 97 |
| 4 | aaab | 97 | 97 |
| 5 | aab | 97 | 97 |
| 3 | baaab | 98 | 97 |
| 2 | abaaab | 97 | 98 |
| 6 | ab | 97 | 98 |
- 按照第一关键字排序:
| 编号 | 前缀 | 排名 | 第二关键字排名 |
|---|---|---|---|
| 1 | aabaaab | 97 | 97 |
| 4 | aaab | 97 | 97 |
| 5 | aab | 97 | 97 |
| 2 | abaaab | 97 | 98 |
| 6 | ab | 97 | 98 |
| 7 | b | 98 | 0 |
| 3 | baaab | 98 | 97 |
-
长度为 $2$ 的子串就排序好了。
我们对排名进行去重时, 只需要判断上下两个前缀的排名与第二关键字排名是否都相等就可以了。
| 编号 | 前缀 | 排名 |
|---|---|---|
| 1 | aabaaab | 1 |
| 4 | aaab | 1 |
| 5 | aab | 1 |
| 2 | abaaab | 2 |
| 6 | ab | 2 |
| 7 | b | 3 |
| 3 | baaab | 4 |
- 接下来排序长度为 $4$ 的子串:
| 编号 | 前缀 | 排名 | 第二关键字排名 |
|---|---|---|---|
| 1 | aabaaab | 1 | 4 |
| 4 | aaab | 1 | 2 |
| 5 | aab | 1 | 3 |
| 2 | abaaab | 2 | 1 |
| 6 | ab | 2 | 0 |
| 7 | b | 3 | 0 |
| 3 | baaab | 4 | 1 |
- 按照第二关键字排序:
| 编号 | 前缀 | 排名 | 第二关键字排名 |
|---|---|---|---|
| 6 | ab | 2 | 0 |
| 7 | b | 3 | 0 |
| 2 | abaaab | 2 | 1 |
| 3 | baaab | 4 | 1 |
| 4 | aaab | 1 | 2 |
| 5 | aab | 1 | 3 |
| 1 | aabaaab | 1 | 4 |
- 按照第一关键字排序:
| 编号 | 前缀 | 排名 | 第二关键字排名 |
|---|---|---|---|
| 4 | aaab | 1 | 2 |
| 5 | aab | 1 | 3 |
| 1 | aabaaab | 1 | 4 |
| 6 | ab | 2 | 0 |
| 2 | abaaab | 2 | 1 |
| 7 | b | 3 | 0 |
| 3 | baaab | 4 | 1 |
- 长度为 $4$ 的子串就排序好了。 进行去重:
| 编号 | 前缀 | 排名 |
|---|---|---|
| 4 | aaab | 1 |
| 5 | aab | 2 |
| 1 | aabaaab | 3 |
| 6 | ab | 4 |
| 2 | abaaab | 5 |
| 7 | b | 6 |
| 3 | baaab | 7 |
- 接下来对长度为 $8$ 的子串进行排序:
| 编号 | 前缀 | 排名 | 第二关键字排名 |
|---|---|---|---|
| 4 | aaab | 1 | 0 |
| 5 | aab | 2 | 0 |
| 1 | aabaaab | 3 | 2 |
| 6 | ab | 4 | 0 |
| 2 | abaaab | 5 | 4 |
| 7 | b | 6 | 0 |
| 3 | baaab | 7 | 6 |
- 对第二关键字进行排序:
| 编号 | 前缀 | 排名 | 第二关键字排名 |
|---|---|---|---|
| 4 | aaab | 1 | 0 |
| 5 | aab | 2 | 0 |
| 6 | ab | 4 | 0 |
| 7 | b | 6 | 0 |
| 1 | aabaaab | 3 | 2 |
| 2 | abaaab | 5 | 4 |
| 3 | baaab | 7 | 6 |
- 对第一关键字进行排序:
| 编号 | 前缀 | 排名 | 第二关键字排名 |
|---|---|---|---|
| 4 | aaab | 1 | 0 |
| 5 | aab | 2 | 0 |
| 1 | aabaaab | 3 | 2 |
| 6 | ab | 4 | 0 |
| 2 | abaaab | 5 | 4 |
| 7 | b | 6 | 0 |
| 3 | baaab | 7 | 6 |
- 进行去重:
| 编号(即 $sa$) | 前缀 | 排名 |
|---|---|---|
| 4 | aaab | 1 |
| 5 | aab | 2 |
| 1 | aabaaab | 3 |
| 6 | ab | 4 |
| 2 | abaaab | 5 |
| 7 | b | 6 |
| 3 | baaab | 7 |
至此, 排序完成, 后缀数组就求出来了。
因为一共进行了 $O(\log n)$ 次排序, 每一次排序复杂度均为 $O(n)$, 所以总复杂度为 $O(n\log n)$。
此份实现可参考 OI-Wiki 的代码。
另外附一个演示动画:
然而这样还不是最优秀的, 有很大的优化空间。
首先你有没有发现, 当运行到第 9 步时, 其实就已经排序完成了?
也就是当排名互不相同时, 我们就可以直接跳出循环, 结束排序了。
并且, 我们每次都对第二关键字进行排序, 又对第一关键字进行排序, 但是在对第二关键字排序前, 第一关键字就已经是有序的了。 我们可不可以利用这一点进行优化?
考虑空串在第二关键字中一定排在前面, 而非空串在第二关键字排序好后又一定和第一关键字排好序时的位置关系是相同的, 所以我们可以直接按照第二关键字有序的顺序来处理第一关键字, 这样只需要对第一关键字进行排序就可以了。
具体实现如下:
int tp[MAX]; // tp 为临时用来存储要进行排序的第一关键字的数组。
int p; // p 用来记录已经加入了几个数。
for (int i = 1; i <= w; i++) tp[++p] = n - w + i;
for (int i = 1; i <= n; i++)
if (sa[i] > w) tp[++p] = sa[i] - w;
// 当 sa[i] 大于 w 的时候, 说明 i 后缀有第二关键字。
这样我们再直接对 $tp$ 数组进行排序, 就可以完成排序了。 虽然复杂度不变, 但是常数优化了许多。
另外, 每一次进行排序的值域是会变的, 可以每一轮排序开头进行优化, 还有一些零碎的优化放到代码注释里吧:
int sa[MAXN], rnk[MAXN], tmp[MAXN], tp[MAXN];
int cnt[MAXN];
int n, m = 300;
char ch[MAXN];
void getSuffixArray() {
auto cmp = [](int a, int b, int w) { // 减少内存的非连续访问
return tp[a] == tp[b] && tp[a + w] == tp[b + w];
};
for (int i = 1; i <= n; i++) cnt[rnk[i] = ch[i]]++;
for (int i = 1; i <= m; i++) cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--) sa[cnt[rnk[i]]--] = i;
for (int w = 1, p = 0; ; w <<= 1, m = p, p = 0) {
// m 为基数排序的值域, 因为一共有 p 种 rank, 所以值域可以更新为 p
for (int i = 1; i <= w; i++) tp[++p] = n - w + i;
for (int i = 1; i <= n; i++) if (sa[i] > w) tp[++p] = sa[i] - w;
for (int i = 1; i <= m; i++) cnt[i] = 0;
for (int i = 1; i <= n; i++) cnt[tmp[i] = rnk[tp[i]]]++;
// 将 rnk[tp[i]] 存入数组, 同样减少内存非连续访问
for (int i = 1; i <= m; i++) cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--) sa[cnt[tmp[i]]--] = tp[i];
swap(tp, rnk); p = 0;
// 这里 tp数组就没用了, 我们需要存上一轮的 rnk 数组, 所以直接swap就可以了。
for (int i = 1; i <= n; i++) rnk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
if (p == n) { // 如果 rnk 互不相同, 直接结束排序。
for (int i = 1; i <= n; i++) sa[rnk[i]] = i;
return;
}
}
}
int main() {
scanf("%s", ch + 1);
n = strlen(ch + 1);
getSuffixArray();
for (int i = 1; i <= n; i++) printf("%d ", sa[i]);
printf("\n");
return 0;
}
$O(n)$ 算法
考场能想起来 $O(n\log n)$ 怎么打就不错了
DC3 算法
参见: [2009]后缀数组——处理字符串的有力工具 by. 罗穗骞
SA-IS 算法
参见: 诱导排序与 SA-IS 算法
应用
说了这么多, 终于要来看他的应用了。
查询子串
这是一个很基本的应用。
一个字符串的子串可以看作是这个字符串一个后缀的前缀。 而我们已经对所有的后缀排好了序, 所以我们可以直接进行二分查找。
对于在字符串中的多次出现, 我们可以在模式串的末尾加一个很小的字符, 找到第一个比它大的, 再加一个很大的字符, 找到第一个比他大的, 这个区间内就都是以模式串为前缀的后缀。
由于单次比较字符串是 $O(n)$ 的, 所以总复杂度就是 $O(n \log n)$。
$\mathrm LCP$(最长公共前缀)
在看这个问题之前, 我们先来看另一个问题:
$height$ 数组
定义: $height_i = lcp(sa_i, sa_{i - 1})$, 即第 $i$ 名前缀与第 $i - 1$ 名前缀的最长公共前缀长度。(特别的, $height_1=0$。)
如何求这个东西呢?
有这样一个定理: $height[rank_i] \ge height[rank_{i - 1}] - 1$。
为什么呢? 我们不妨设后缀 $i - 1$ 为 $aSB$, 后缀 $sa[rank_{i - 1} - 1]$ 为 $aSA$, 那么 $height[rank_{i - 1}] = \mid S\mid + 1$。
则后缀 $i$ 为 $SB$, 后缀 $sa[rank_{i-1} - 1] + 1$ 为 $SA$, 那么后缀 $sa[rank_{i-1}-1] + 1$ 一定排在后缀 $i$ 前面, 那么 $sa[rank_i-1]$ 一定就有 $S$ 这个前缀, 那么就可以说明上面的定理了。
有了这个定理, 求 $height$ 数组就简单多了, 这里放一个代码, 自己看一下就能明白了。
void getHeight() {
for (int i = 1, k = 0; i <= n; i++) {
if (k) k--;
while (s[i + k] == s[sa[rnk[i] - 1] + k]) k++;
height[rnk[i]] = k;
}
}
我们再回来看 $\mathrm LCP$ 问题。 既然我们求得了相邻两个字符串的 $\mathrm LCP$ 那么我们将两个前缀之间的所有 $height$ 数组取 $\min$, 就是这两个前缀的 $\mathrm LCP$ 了。
更准确点来说, $\displaystyle lcp(i, j) = \min_{k=rank_i + 1}^{rank_j} height_k$
这样就将 $\mathrm LCP$ 问题转换为了 $\mathrm RMQ$ 问题。
比较两个子串大小
我们只需要去比较两个子串为开头的后缀的 $\mathrm LCP$。 如果 $\mathrm LCP$ 的长度大于两个字串的长度, 那么说明两个子串相等; 否则, 只需要比较两个后缀的排名就可以比较出两个子串的大小了。
不同子串的数目
子串就是后缀的前缀,所以可以枚举每个后缀,计算前缀总数,再减掉重复。
前缀总数其实就是子串个数,为 $\displaystyle\frac{n(n+1)}{2}$。
如果按后缀排序的顺序枚举后缀,每次新增的子串就是除了与上一个后缀的 $\mathrm LCP$ 剩下的前缀。这些前缀一定是新增的,否则会破坏上述 $\mathrm LCP$ 的性质。只有这些前缀是新增的,因为 $\mathrm LCP$ 部分在枚举上一个前缀时计算过了。
所以答案为:
\[\frac{n(n+1)}{2}-\sum_{i=2}^nheight_i\]